Integration of Exponential Functions from First Principles

Integration from First Principles

Foreword: In this part of the paper, I explain how to integrate Exponential Functions from First Principles. (Use the latest Mozilla Firefox Browser, to see the equations properly.)

By: Chrysanthus Date Published: 27 Jun 2019

Introduction

In this part of the paper, I explain how to integrate Exponential Functions from First Principles. You should have read the previous parts of the series before reaching here, as this is the continuation.

Integration is area under the curve.
Consider the following diagram:

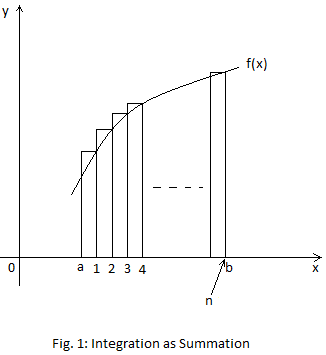
y = f(x)

You might have seen the following:

\int_{a}^{b} f (x) d x = \lim_{δ x \to 0} \sum_{x = a}^{x = b} f (x) δ x

This statement is not perfect. It should actually be:

\int_{a}^{b} f (x) d x = \lim_{δ x \to 0} \sum_{x = a}^{x = b} f (x_{n}) δ x

where f(x_n) is a particular height from the curve to the x-axis.

My Discovery

The widths of the vertical strips are equal.

As 𝛿x turns to 0, the number of strips increases.

n is the total number of strips.

δ x = \frac{b - a}{n}

As 𝛿x → 0, n → ∞

The series and the formula for its summation, for all the heights of the strips from a to b, is obtained. If you do not know the formula for the series, develop one, and that may take time. Summing is done for the heights, from 1 to n.

The summation expression above in the statement, is replaced with the summation formula.

As n → ∞ the right-hand-side of the statement becomes the definite integral; and that concludes the scheme.

Let total area be represented by A. So, my statement for the Integration from First Principles is:

A = \lim_{n \to \infty} \sum_{x = a}^{x = b} f (x_{n}) \frac{b - a}{n}

In the following analysis, Taylor series expansion and the definite integral for the polynomial term, have been used.

Integration of the Function, e^x

Let the definite integral be represented by A, and let the indefinite integral be represented by I.

Here,

y = e^x

i.e.

f(x) = e^x

The Taylor series expansion of e^x about x = 0 is:

e^{x} = 1 + \frac{x^{1}}{1!} + \frac{x^{2}}{2!} + \frac{x^{3}}{3!} + \dots \infty

The general formula to integrate a polynomial term, from x=a to x=b, from First Principles is:

A = C [\frac{1}{(m + 1)} b^{(m + 1)} - \frac{1}{(m + 1)} a^{(m + 1)}]

Applying this to the above Taylor series expansion (integrating the R.H.S) gives:

A = b - a + \frac{b^{2}}{2!} - \frac{a^{2}}{2!} + \frac{b^{3}}{3!} - \frac{a^{3}}{3!} + \frac{b^{4}}{4!} - \frac{a^{4}}{4!} + \dots \infty

Rearranging:

∴ A = b + \frac{b^{2}}{2!} + \frac{b^{3}}{3!} + \frac{b^{4}}{4!} + \dots \infty - a - \frac{a^{2}}{2!} - \frac{a^{3}}{3!} - \frac{a^{4}}{4!} - \dots \infty

Add 1 and subtract 1 appropriately:

\Rightarrow A = 1 + b + \frac{b^{2}}{2!} + \frac{b^{3}}{3!} + \frac{b^{4}}{4!} + \dots \infty - 1 - a - \frac{a^{2}}{2!} - \frac{a^{3}}{3!} - \frac{a^{4}}{4!} - \dots \infty

Grouping:

\Rightarrow A = [1 + b + \frac{b^{2}}{2!} + \frac{b^{3}}{3!} + \frac{b^{4}}{4!} + \dots \infty] - [1 + a + \frac{a^{2}}{2!} + \frac{a^{3}}{3!} + \frac{a^{4}}{4!} + \dots \infty]

Each group is a Taylor series expansion of the exponential function about variable = 0:

∴ A = e^{b} - e^{a} �������.the definite integral

Now, there is no value of a, for which we can have the indefinite integral, of the type resulting from the reversal of differentiation, which is e^x. So, I have chosen 0 for a, and x for b.

If b = x and a = 0,

∴ I = e^{x} - 1 �������.the indefinite integral from First Principles

Integration of the Function, w^x

Let the definite integral be represented by A, and let the indefinite integral be represented by I.

Here,

y = w^x

i.e.

f(x) = w^x

where w is a base other than e.

Let w^x = e^z

where z is the index that enables the equality.

∴ ln(w^x) = ln(e^z)

⇒ xln(w) = zln(e)

⇒ z = xln(w)

∴ w^x = e^xln(w)

The Taylor series expansion of e^xln(w) about x = 0 is:

e^{x \ln w} = 1 + \frac{\ln^{1} w x^{1}}{1!} + \frac{\ln^{2} w x^{2}}{2!} + \frac{\ln^{3} w x^{3}}{3!} + \dots \infty

The general formula to integrate a polynomial term, from x=a to x=b, from First Principles is:

A = C [\frac{1}{(m + 1)} b^{(m + 1)} - \frac{1}{(m + 1)} a^{(m + 1)}]

Applying this to the above Taylor series (integrating the R.H.S) gives:

A = b - a + \frac{\ln^{1} w b^{2}}{2!} - \frac{\ln^{1} w a^{2}}{2!} + \frac{\ln^{2} w b^{3}}{3!} - \frac{\ln^{2} w a^{3}}{3!} + \frac{\ln^{3} w b^{4}}{4!} - \frac{\ln^{3} w a^{4}}{4!} + \dots \infty

Rearranging:

∴ A = b + \frac{\ln^{1} w b^{2}}{2!} + \frac{\ln^{2} w b^{3}}{3!} + \frac{\ln^{3} w b^{4}}{4!} + \dots \infty - a - \frac{\ln^{1} w a^{2}}{2!} - \frac{\ln^{2} w a^{3}}{3!} - \frac{\ln^{3} w a^{4}}{4!} - \dots \infty

Multiplying R.H.S by lnw/lnw, which is equal to 1, gives

\Rightarrow A = \frac{\ln w}{\ln w} [b + \frac{\ln^{1} w b^{2}}{2!} + \frac{\ln^{2} w b^{3}}{3!} + \frac{\ln^{3} w b^{4}}{4!} + \dots \infty - a - \frac{\ln^{1} w a^{2}}{2!} - \frac{\ln^{2} w a^{3}}{3!} - \frac{\ln^{3} w a^{4}}{4!} - \dots \infty]

Multiplying each term on the R.H.S by the numerator, lnw gives:

\Rightarrow A = \frac{1}{\ln w} [\ln w b + \frac{\ln^{2} w b^{2}}{2!} + \frac{\ln^{3} w b^{3}}{3!} + \frac{\ln^{4} w b^{4}}{4!} + \dots \infty - \ln w a - \frac{\ln^{2} w a^{2}}{2!} - \frac{\ln^{3} w a^{3}}{3!} - \frac{\ln^{4} w a^{4}}{4!} - \dots \infty]

Add 1 and subtract 1 appropriately:

\Rightarrow A = \frac{1}{\ln w} [1 + \ln w b + \frac{\ln^{2} w b^{2}}{2!} + \frac{\ln^{3} w b^{3}}{3!} + \frac{\ln^{4} w b^{4}}{4!} + \dots \infty - 1 - \ln w a - \frac{\ln^{2} w a^{2}}{2!} - \frac{\ln^{3} w a^{3}}{3!} - \frac{\ln^{4} w a^{4}}{4!} - \dots \infty]

Grouping:

\Rightarrow A = \frac{1}{\ln w} [1 + \ln w b + \frac{\ln^{2} w b^{2}}{2!} + \frac{\ln^{3} w b^{3}}{3!} + \frac{\ln^{4} w b^{4}}{4!} + \dots \infty] - [1 + \ln w a + \frac{\ln^{2} w a^{2}}{2!} + \frac{\ln^{3} w a^{3}}{3!} + \frac{\ln^{4} w a^{4}}{4!} + \dots \infty]

Each group is a Taylor series expansion of the exponential function about variable = 0:

∴ A = \frac{1}{\ln w} e^{b \ln w} - \frac{1}{\ln w} e^{a \ln w} �������.the definite integral

Now, there is no value of a, for which we can have the indefinite integral, of the type resulting from the reversal of differentiation, which is 1/linw[e^xlnw]. So, I have chosen 0 for a, and x for b.

If b = x and a = 0,

∴ A = \frac{1}{\ln w} e^{b \ln w} - 1 �������.the indefinite integral from first principles

Integration of the Function, e^(px+q)

Let the definite integral be represented by A, and let the indefinite integral be represented by I.

Here,

y = e^(px+q)

i.e.

f(x) = e^(px+q)

The Taylor series expansion of e^(px+q) about x = -q/p is:

e^{x \ln w} = 1 + \frac{{(p x + q)}^{1}}{1!} + \frac{{(p x + q)}^{2}}{2!} + \frac{{(p x + q)}^{3}}{3!} + \dots \infty

The general formula to integrate the function (px+q)^m, from x=a to x=b, from First Principles is:

A = \frac{1}{(m + 1) p} {(p b + q)}^{(m + 1)} - \frac{1}{(m + 1) p} {(p a + q)}^{(m + 1)}

Applying this to the above Taylor series (integrating the R.H.S) gives:

A = b - a + \frac{{(p b + q)}^{2}}{2! p} - \frac{{(p a + q)}^{2}}{2! p} + \frac{{(p b + q)}^{3}}{3! p} - \frac{{(p a + q)}^{3}}{3! p} + \frac{{(p b + q)}^{4}}{4! p} - \frac{{(p a + q)}^{4}}{4! p} + \dots \infty

Rearranging:

∴ A = b + \frac{{(p b + q)}^{2}}{2! p} + \frac{{(p b + q)}^{3}}{3! p} + \frac{{(p b + q)}^{4}}{4! p} + \dots \infty - a - \frac{{(p a + q)}^{2}}{2! p} - \frac{{(p a + q)}^{3}}{3! p} - \frac{{(p a + q)}^{4}}{4! p} - \dots \infty

Factorizing out 1/p, gives

\Rightarrow A = \frac{1}{p} [b p + \frac{{(p b + q)}^{2}}{2!} + \frac{{(p b + q)}^{3}}{3!} + \frac{{(p b + q)}^{4}}{4!} + \dots \infty - a p - \frac{{(p a + q)}^{2}}{2!} - \frac{{(p a + q)}^{3}}{3!} - \frac{{(p a + q)}^{4}}{4!} - \dots \infty]

Add 1 and subtract 1 appropriately; also add q and subtract q appropriately:

\Rightarrow A = \frac{1}{p} [1 + b p + q + \frac{{(p b + q)}^{2}}{2!} + \frac{{(p b + q)}^{3}}{3!} + \frac{{(p b + q)}^{4}}{4!} + \dots \infty - 1 - a p - q - \frac{{(p a + q)}^{2}}{2!} - \frac{{(p a + q)}^{3}}{3!} - \frac{{(p a + q)}^{4}}{4!} - \dots \infty]

Grouping:

\Rightarrow A = \frac{1}{p} [1 + b p + q + \frac{{(p b + q)}^{2}}{2!} + \frac{{(p b + q)}^{3}}{3!} + \frac{{(p b + q)}^{4}}{4!} + \dots \infty] - [1 - a p - q - \frac{{(p a + q)}^{2}}{2!} - \frac{{(p a + q)}^{3}}{3!} - \frac{{(p a + q)}^{4}}{4!} - \dots \infty]

Each group is a Taylor series expansion of the exponential function about variable = 0:

∴ A = \frac{1}{p} e^{(p x + q)} - \frac{1}{p} e^{(p x + q)} �������.the definite integral

Now, there is no value of a, for which we can have the indefinite integral, of the type resulting from the reversal of differentiation, which is (1/p)e^(px+q). So, I have chosen 0 for -q/p, and x for b.

If b = x and a = 0,

∴ A = \frac{1}{p} e^{(p x + q)} - \frac{1}{p} �������.the indefinite integral from first principles

Integration of the Function, w^(px+q)

Let the definite integral be represented by A, and let the indefinite integral be represented by I.

Here,

y = w^(px+q)

i.e.

f(x) = w^(px+q)

where w is a base other than e.

Let w^(px+q) = e^z

where z is the index that enables the equality.

∴ ln(w^(px+q)) = ln(e^z)

⇒ (px+q)ln(w) = zln(e)

⇒ z = (px+q)ln(w)

∴ w^x = e^ln(w)(px+q)

∴ w^x = e^{(pln(w)x+qln(w))}

The Taylor series expansion of e^{(pln(w)x+qln(w))} about x = -qln(w)/pln(w) is:

e^{(p \ln w + q \ln w)} = 1 + \frac{{(p \ln (w) x + q \ln (w))}^{1}}{1!} + \frac{{(p \ln (w) x + q \ln (w))}^{2}}{2!} + \frac{{(p \ln (w) x + q \ln (w))}^{3}}{3!} + \dots \infty

The general formula to integrate the function (px+q)^m, from x=a to x=b, from First Principles is:

A = \frac{1}{(m + 1) p} {(p b + q)}^{(m + 1)} - \frac{1}{(m + 1) p} {(p a + q)}^{(m + 1)}

Applying this to the above Taylor series (integrating the R.H.S) gives:

A = b - a + \frac{{(p \ln (w) b + q \ln w)}^{2}}{2! p \ln w} - \frac{{(p \ln (w) a + q \ln w)}^{2}}{2! p \ln w} + \frac{{(p \ln (w) b + q \ln w)}^{3}}{3! p \ln w} - \frac{{(p \ln (w) a + q \ln w)}^{3}}{3! p \ln w} + \frac{{(p \ln (w) b + q \ln w)}^{4}}{4! p \ln w} - \frac{{(p \ln (w) a + q \ln w)}^{4}}{4! p \ln w} + \dots \infty

Rearranging:

∴ A = b + \frac{{(p \ln (w) b + q \ln w)}^{2}}{2! p \ln w} + \frac{{(p \ln (w) b + q \ln w)}^{3}}{3! p \ln w} + \frac{{(p \ln (w) b + q \ln w)}^{4}}{4! p \ln w} + \dots \infty - a - \frac{{(p \ln (w) a + q \ln w)}^{2}}{2! p \ln w} - \frac{{(p \ln (w) a + q \ln w)}^{3}}{3! p \ln w} - \frac{{(p \ln (w) a + q \ln w)}^{4}}{4! p \ln w} - \dots \infty

Factorizing out 1/p, gives

\Rightarrow A = \frac{1}{p \ln w} [b p \ln w + \frac{{(p \ln (w) b + q \ln w)}^{2}}{2!} + \frac{{(p \ln (w) b + q \ln w)}^{3}}{3!} + \frac{{(p \ln (w) b + q \ln w)}^{4}}{4!} + \dots \infty - a p \ln w - \frac{{(p \ln (w) a + q \ln w)}^{2}}{2!} - \frac{{(p \ln (w) a + q \ln w)}^{3}}{3!} - \frac{{(p \ln (w) a + q \ln w)}^{4}}{4!} - \dots \infty]

Add 1 and subtract 1 appropriately; also add qlnw and subtract qlnw appropriately:

\Rightarrow A = \frac{1}{p \ln w} [1 + b p \ln w + q \ln w + \frac{{(p \ln (w) b + q \ln w)}^{2}}{2!} + \frac{{(p \ln (w) b + q \ln w)}^{3}}{3!} + \frac{{(p \ln (w) b + q \ln w)}^{4}}{4!} + \dots \infty - 1 - a p \ln w - q \ln w - \frac{{(p \ln (w) a + q \ln w)}^{2}}{2!} - \frac{{(p \ln (w) a + q \ln w)}^{3}}{3!} - \frac{{(p \ln (w) a + q \ln w)}^{4}}{4!} - \dots \infty]

Grouping:

\Rightarrow A = \frac{1}{p \ln w} [1 + b p \ln w + q \ln w + \frac{{(p \ln (w) b + q \ln w)}^{2}}{2!} + \frac{{(p \ln (w) b + q \ln w)}^{3}}{3!} + \frac{{(p \ln (w) b + q \ln w)}^{4}}{4!} + \dots \infty] - [1 - a p \ln w + q \ln w - \frac{{(p \ln (w) a + q \ln w)}^{2}}{2!} - \frac{{(p \ln (w) a + q \ln w)}^{3}}{3!} - \frac{{(p \ln (w) a + q \ln w)}^{4}}{4!} - \dots \infty]

Each group is a Taylor series expansion of the exponential function about variable = 0:

∴ A = \frac{1}{p \ln w} e^{\ln w (p x + q)} - \frac{1}{p \ln w} e^{\ln w (p x + q)} �������.the definite integral

If b = x and a = 0,

∴ A = \frac{1}{p \ln w} e^{\ln w (p x + q)} - \frac{1}{p \ln w} �������.the indefinite integral from first principles

This is the end of this part of the series. Continue in the next part.

Chrys

Cousins

BACK

Broad Network

Series Articles

Integration of Exponential Functions from First Principles

Integration from First Principles

Introduction

My Discovery

Related Links

Cousins

Comments