Bases for Integration from First Principles
Introduction to Integration from First Principles
Foreword: This paper introduces you to my discovery of Integration from First Principles. (Refresh your page in case all the formulas are not downloaded)
Copyright/Patent: All rights reserved!
By: Chrysanthus Date Published: 21 Mar 2019
Introduction
Integration is area under the curve.
Consider the following diagram:
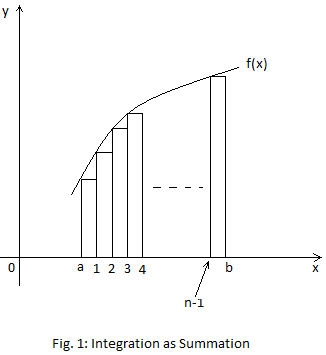
y = f(x)
You might have seen the following:
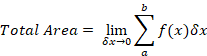
This statement is not perfect. It should actually be:
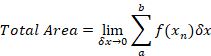
where f(xn) is a particular height from the curve to the x-axis.
My Discovery
The widths of the vertical strips are equal.
As 𝛿x turns to 0, the number of strips increases.
n is the total number of strips.
![]()
As 𝛿x → 0, n → ∞.
The series and the formula for its summation, for all the heights of the strips from a to b, is obtained. If you do not know the formula for the series, develop one, and that may take time. Summing can be done for the heights, from 0 to n-1.
The summation expression above in the statement, is replaced with the summation formula.
As n → ∞, the right-hand-side of the statement becomes the definite integral; and that concludes the scheme.
Let total area be represented by A. So, my statement for the Integration from First Principles is:
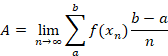
Integration of the Constant, C
Let the definite integral be represented by A, and let the indefinite integral be represented by I. Let the summation expression (discrete summation) be Sn.
Here,
y = C
i.e.
f(x) = C
Sn = (C0 + C + C + C + - - - + Cn-1)𝛿x
= (nC) 𝛿x
But ![]()
⸫
Sn = ![]()
The ns cancel:
=> Sn = C(b - a)
=> Cb - Ca
As n → ∞,
A = Cb -Ca ………………….the definite integral
If a is 0 and b is x,
I = Cx ………………………..the indefinite integral
Integration of y = x
That is,
f(x) = x
Sn = [a + (a+𝛿x) + (a+2𝛿x) + (a+3𝛿x) + - - - + (a+(n-1)𝛿x)]𝛿x
The series in square brackets is an Arithmetic Progression, with first term = a and common difference = 𝛿x.
![]()
![]()
But
![]()
![]()
![]()
As n → ∞,
![]()
![]()
![]()
If a is 0 and b is x,
![]()
Integration of y=x2
That is,
f(x) = x2
Sn = [(a+0𝛿x)2 + (a+1𝛿x)2 + (a+2𝛿x)2 + (a+3𝛿x)2 + - - - + (a+(n-1)𝛿x)2]𝛿x
=> Sn = [a2
+ a2 + 2a𝛿x + 𝛿2x
+ a2 + 4a𝛿x + 4𝛿2x
+ a2 + 6a𝛿x + 9𝛿2x
+
.
.
+ a2 + 2a(n-1)𝛿x + (n-1)2𝛿2x]𝛿x
=> Sn = [a2 + a2 + a2 + a2 + - - - +aan
+ 2a𝛿x + 4a𝛿x + 6a𝛿x + - - - + 2a(n-1)𝛿x
+ 1𝛿2x + 4𝛿2x + 9𝛿2x + - - - + (n-1)2𝛿2x]𝛿x
The first row in square brackets gives, na2.
The second row is an Arithmetic Progression, with first term = 0 and common difference = 2a𝛿x, giving,
![]()
![]()
The third row is,
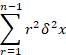
A common formula for the r2 series is,
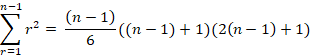
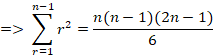
![]()
![]()
![]()
But
![]()
![]()
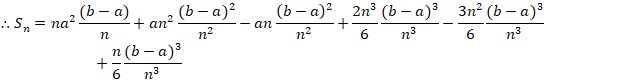
![]()
As n → ∞,
![]()
![]()
![]()
After subtractions, we have,
![]()
If a is 0 and b is x,
![]()
Integration of y=x3
That is,
f(x) = x3
Sn = [(a+0𝛿x)3 + (a+1𝛿x)3 + (a+2𝛿x)3 + (a+3𝛿x)3 + - - - + (a+(n-1)𝛿x)3]𝛿x
=> Sn = [a3
+ a3 + 3a2𝛿x + 3a𝛿2x + 𝛿3x
+ a3 + 3(21)a2𝛿x + 3(22)a𝛿2x + (23)𝛿3x
+ a3 + 3(31)a2𝛿x + 3(32)a𝛿2x + (33)𝛿3x
+
.
.
+ a3 + 3(n-1)a2𝛿x + 3(n-1)2a𝛿2x + (n-1)3𝛿3x]𝛿x
=> Sn = [a3 + a3 + a3 + a3 + - - - +a3n
+ 3a2𝛿x + 3(31)a2𝛿x + 3(31)a2𝛿x + - - - + 3(n-1)a2𝛿x
+ 3a𝛿2x + 3(22)a𝛿2x + 3(32)a𝛿2x + - - - + 3(n-1)2a𝛿2x
+ 𝛿3x + (23)𝛿3x + (33)𝛿3x + - - - + (n-1)3𝛿3x]𝛿x
The first row in square brackets gives, na3.
The second row is an Arithmetic Progression, with first term = 0 and common difference = 3a2𝛿x, giving,
![]()
![]()
The third row is,
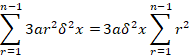
A common formula for the r2 series is,
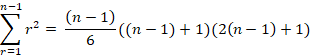
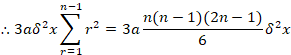
![]()
The fourth row is,
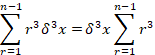
A common formula for the r3 series is,
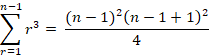
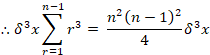
![]()
![]()
![]()
But
![]()
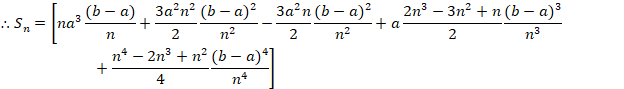
As n → ∞,
![]()
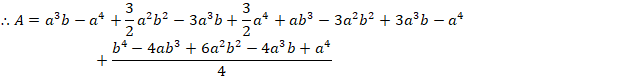
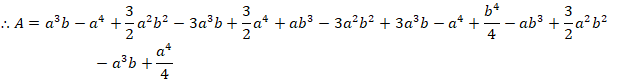
After subtractions and additions, we have,
![]()
If a is 0 and b is x,
![]()
Do we have to continue looking for the summation of each power series: x4, x5, x6, etc.? – No! Wait for the complete paper before the end of next month, which has my power series for xn.
The Complete Paper
I will publish the complete paper, which solves different types of integrations, taught for pure and further math in Anglo-Saxon high schools, from First Principles; before the end of next month. I will publish the full paper in this website.
Chrys
Related Links
Complete Paper for the Integration from First PrinciplesMore Related Links